2019. 11. 30. 15:55ㆍ학교공부/지능시스템

다음과 같은 experiments들이 수행되었다고 보자.
그렇다면 HEADACHE = true, FEVER = false, VOMITING = true일때에 Meningtis는 어떻게될까?
1. Bayesian Product
Bayesian prediction을 생성하기 위해서, target feature t에 대한 확률을 생성할 것이다. 주어진 값들은 descriptive features이다. 이와 Baye's Theorem을 이용해서 more than one piece of evidence를 받아올 수 있도록 할 것이다.
P(t = l | q) = ?
Generalized Baye's Theorem은 아래와 같다.

Generalized Baye's theorem을 이용하기 위해, 우리는 세가지의 확률을 계산해야한다.
1) P(t=l), prior probability of target feature t taking the level l
2) P(q[1],...,q[m]) : joint probability of the descriptive features of a query instance
3) P(q[1],...,q[m]|t = l), conditional probability of the descriptive feature of a query instance taking a specific set of values given that the target feature takes the level l
1)과 2)는 계산하기 쉽다. P(t=l)은 relative frequency with target feature (=l) in a dataset이다.
P(q[1],...,q[m])은 relative frequency in a dataset of the joint event that descriptive features take q[1]...q[m]이다.
또한 Total probability로도 계산된다.
3)은 dataset으로부터 직접적으로 계산하거나, chain rule로 계산할 수 있다.

위의 3)에 chain rule을 이용학히 위해서, 다음과 같이 쓴다.

예를 들어보자.

Baye's Theorem으로, 위 문제는 다음과 같이 변형될 수 있다.

MENINGTIS에는 true 혹은 false의 두 값밖에 없기에, 이 계산을 두번 수행해야 한다.

위 dataset에서, .
P(m)은 true가 3개, false가 7개이므로 P(m) = 0.3이다.
p(h, ~f, v)는 true, false, true인 event가 총 6개, 전체 event가 10개이므로 p(h,~f,v)는 0.6이다.
그러면 P(h,~f,v | m)은 chain rule을 이용해서 구한다.

P(h|m)은 m이 true일때 h가 true일 경우, 즉 0.66
P(~f|h,m)은 h,m이 true일 때 f가 false인 경우, 즉 1
P(v|~f,h,m)은 f가 false, h,m이 true일 때 v가 true인 경우, 즉 1
따라서 0.66이 된다.
결국 P(m|h,~f,v)는 0.66 * 0.3 / 0.6 = 0.3333이 된다.
이번에는 P(~m|h,~f,v)를 계산한다. 계산해보면 0.6667이 된다.
따라서, 환자가 두통 및 구토 증상이 있더라도 meningtis에 걸리지 않았을 확률이 걸렸을 확률의 두배라는 결론을 얻는다.
그렇다면 이 계산된 확률 결과값으로부터 어떻게 final decision을 내리는 것일까?
prediction model이 highest posterior probability(maximum aposteriori(MAP) prediction)을 가지는 target level을 return하도록 한다.

즉 위 예제에서는 ~m일때가 더 컸으므로, m=false를 출력하는 것이다.
다른 예제를 살펴보자.
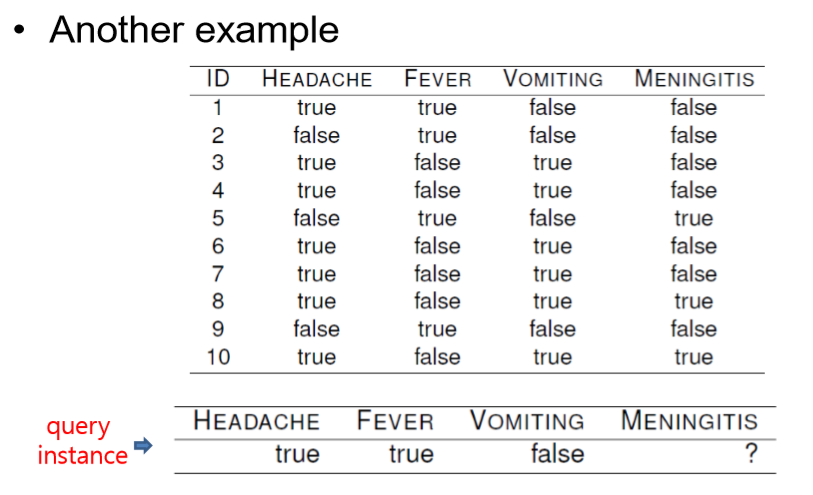
먼저 P(m | h,f,~v)는 0,
P(~m|h,f,~v) 는 1이다.
따라서 meniningtis에 걸리지 않았다고 출력한다.
이 방법에 문제는 우리의 dataset이 충분히 크지 않아 meningtis diagnosis scenario의 representative라 보기 힘들다는 것이다. 실제로는 모든 possible combinations of descriptive features를 모으는건 거의 불가능하다.
* Curse of Dimensionality : descrptive features의 수가 늘수록 potential conditioning events의 수가 exponentially 증가하게 된다. 즉 새로운 descriptive feature가 추가되면 dataset의 크기도 exponentially increase를 요한다는 것이다.
Conditinal independence와 factorization이 이러한 문제를 해결하기에 도움을 줄 수 있다.