2019. 12. 1. 15:01ㆍ학교공부/암호공학
Keyword : Digital Signature, RSA, ElGamal, Schnorr, DSS, applications of digital signatures
1. Comparison
: 옛날에는 Signature라는것이 document의 일부였다. 하지만 디지털화 된 문서에 서명을 하기 위해서는 signature을 document와 분리해서 보내야 한다.
Verification Method
: 옛날에는 수신자가 문서를 받으면, document의 signature과 file의 signature을 대조하는 방식으로 인증했다. 하지만 digital signature은, 수신자가 message와 signature을 받고, 수신자가 verification technique을 적용해서 message와 signature을 combine해서 authenticity를 verify해야 한다.
Relationship
: 옛날에는 signature과 document가 one-to-many relationship을 가졌다. digital signature에서는 one-to-one relationship이 존재한다.
Duplicity
: 옛날에는 signed document의 복사본과 original one on file이 구별가능했다. digital signature에서는, factor of the time이 document에 존재하지 않는다면 그러한 distinction은 존재하지 않는다.
2. Process
: 전송자는 signing algorithm을 통해 message의 sign을 한다. message와 signature은 수신자에게 전송되고, 수신자는 메시지와 signature을 받아서 verifying algorithm을 수행한다. 만약 결과값이 true면 message는 accept되고, 아닐경우 reject된다.

디지털 서명은 public-key system을 필요로 한다.

signer은 private key로 sign을 하고, signer's public key를 통해 나중에 verifier가 verify를 수행한다.
만약 document가 signed되면 어떤 사람이든지 verify할 수 있는데, 왜냐하면 모두가 Alice으 public key에는 access할 수 있기 때문이다. 따라서 alice는 public key로 sign을 해선 안된다.
비대칭키 방식은 long message를 이용할 때는 매우 inefficient하다. digital signature system에서의 message는 보통 long message이지만 우리는 비대칭키 방식을 이용해야 한다. 따라서 우리는 message digest를 sign하는 방식을 쓴다. carefully selected message digest는 메시지와 one-to-one relationship을 가지고, 전송자는 digest를 sign하고 수신자는 digest를 verify하게 하면 된다.

3. Services
우리는 이미 여러 security services에 대해 이야기한 적 있다. message confidentiality, message authentication, message integrity와 nonrepudiation이다. digital signature은 message confidentiality를 제외한 이후 3가지 서비스를 제공한다. message confidentiality의 경우는 암호/복호화 서비스가 필요하다.
1) Message Authentication
digital signature이 secure scheme이라면, message authentication을 제공할 수 있다. Bob은 Alice로부터 전송된 메시지를 verify할 수 있고, Alice의 public key로는 Eve의 private key로 signed된 signature을 verify 할 수 없다.
2) Message Integrity
우리가 whole message를 sign하더라도 message의 integrity가 보장되는데 message가 변경되면 same signature이 나우지 않기 때문이다. 오늘날의 digital signature scheme은 hash function을 signing 및 verifying에 이용하는데, 이는 integrity를 제공한다.
3) Nonrepudiation

만약 Alice가 message를 sign하고 나서 deny한다면, Bob은 추후에 Alice가 sign을 했다는 사실을 증명할 수 있을까? 예를들어 Alice가 은행(Bob)에게 말하기를 Ted의 계좌에 그녀의 계좌로부터 $10,000를 인출하여 보내라고 했다고 하자. Alice는 추후에 지시한 사실을 부정할 수 있을까?
하나의 해결 방법은 trusted third party이다. 사람들은 그들간의 trusted party를 생성해서, denial of sent the message를 방지한다. 추후에 Alice가 denies that she sent the message를 하면, center가 copy of the saved message를 보여준다.
4) Confidentiality

digital signature은 privacy는 제공하지 않는다. privacy가 필요하다면, another layer of encryption/decryption이 제공되어야 한다.
4. Attacks On Digital Signature
세 가지의 attacks on digital signature을 볼 것이다. : key-only, known-message, and chosen-message.
1) Key-Only Attack
: Eve는 Alice의 pulbic information에 대한 access만 가지고 있다. Eve는 Alice의 signature을 만들어서 Bob에게 메시지가 마치 Alice에게서부터 온것처럼 위장한다. 이는 암호화 부분에서 설명했던 ciphertext-only attack과 같다.
2) Known-Message Attack
: Eve는 one or more message와 signature pairs에 대한 정보를 가지고 있다. 즉, Alice에 의해 previously signed된 document들에 대한 정보를 가진다. 이는 Known-plaintext attack과 비슷하다.
3) Chosen-Mesage Attack
: Eve는 Alice가 어떤 message를 sign하든지 그에 대한 정보를 가질 수 있다. 즉 Eve는 chosen-message/signature pair를 언제나 볼 수 있다. 이는 Chosen-Plaintext Attack과 비슷하다.
Forgery Types : 만약 Attack이 성공했다면 이제 위조 단계이다. 두 종류의 위조법이 있는데, existential과 selective이다.
4) Existential Forgery
existential forgery에서 Eve는 valid message-signature pair를 생성할 수 있다. 하지만 진짜 쓸만한 건 만들어내지 못할 수 있다. 이러한 종류의 forgery는 있을 수 있으나 Eve는 이로부터 큰 이익을 얻을 순 없다. Eve의 message는 syntatically or semantically unintelligible하다.
5) Selective Forgery
: Selective forgery에서는 Eve가 선택적으로 선택한 컨텐츠의 Alice의 signature on a message를 위조할 수 있다. Eve에게 beneficial하지만, 이러한 종류의 위조방법의 probability는 매우 낮으며, negligible하다.
5. Digital Signature Schemes.
1) RSA Digital Signature Scheme

10장에서 본 RSA이다. RSA는 signing 및 verifying a message에도 이용된다. digital signature scheme은 private과 public key의 역할을 바꾼다.
첫째로, 송신자의 private과 public key가 이용된다.
둘째로, 송신자는 her own private key로 document를 sign한다. 이후 수신자는 송신자의 public key를 통해 verify한다.
RSA digital signature scheme에서의 Key generation 방식은 RSA key generation방식과 완전동일하다.

Alice는 private exponent S= M^d mod n 을 이용해서 message의 signature을 생성하고 Bob에게 signature과 message를 전송한다.
Bob은 M과 S를 받게 되고, Bob은 Alice의 public exponent를 이용해서 copy of message를 만든다. M` = S^e mod n. Bob은 이 copy of message M`과 original message M의 값을 비교하고 둘이 congruent하다면 message를 accept한다.
예제 ) Alice가 p=823, q=953을 선택하고 n=784319를 선택했다. pi(n)의 값은 782544이다. 이제 Alice는 e=313을 선택해서 d=160009를 계산했다. 여기에서 key generation은 끝났다. Alice가 original Message M=19070을 Bob에게 보낸다고 생각해보자. private exponent d =160009를 이용해서 message sign을 수행했다.
M = 19070 -> S = 19070^(160009) mod 784319 = 210625 mod 784319 = 210625
M` = 210625^313 mod 784319 = 19070 mod 784319 -> M` = 19070
M` = M`mod n 이기에 message가 동일하다. 따라서 alice's signature이 verify되었다.
2) RSA Signature on the Message Digest
이번에는 message digest에 RSA signature을 적용할 것이다.
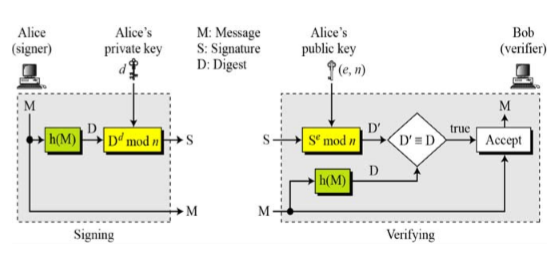
Alice, the signer은 agreed-upon hash function으로 digest를 생성한다. D= h(M)
그리고 digest를 sign한다. S = D^d mod n.
messsage와 signature이 Bob에게 보내진다.
Bob, the verifier은 message와 signature을 받고, Alice의 public exponent를 이용해서 digest를 얻는다.
D` = S^e mod n.
그 이후 hash algorithm을 이용해서 받은 message를 D = h(M)으로 변환시킨다.
Bob이 이제는 D`과 D를 비교하고, 둘이 congruent to modulo n 하다면 message를 accept한다.
3) ElGamal Digital Signature Scheme

signing process에서는 두 function이 두개의 signature을 만든다. verifying process에서는 two functions을 비교한다. f1의 경우에는 signing 및 verifying에 둘다 사용되지만 input이 다르다. 위 그림은 또한 각각의 function에 대한 input도 보여준다. message는 f2의 part of input이다. 그러면서 f1의 verifying단계에서의 part of input이기도 하다. (e1, e2, p)는 Alice의 public key이고, d가 private key이다. 여기서 e2 = e1^d 이다.

Signing:
1. Alice는 secret random number r을 고른다. alice는 new message를 sign할 때 마다 new r이 필요하다.
2. Alice는 첫번째 signature S1 = e1^r mod p 를 계산한다.
3. Alice는 Second signature S2 = (M-d * S1) * r^-1 mod (p-1)을 계산한다. 이 때 r^-1은 multiplicative inverse of r modulo p이다.
4. Alice는 M,S1,S2를 Bob에게 전송한다.
Verifying
1. Bob은 0<S1<p를 만족하는지 확인한다.
2. Bob은 0<S2<p-1을 만족하는지 확인한다.
3. Bob은 V1 = e1^M mod p 를 계산한다.
4. Bob은 V2 = e2^S1 * S1^S2 mod p 를계산한다.
5. V1와 V2가 congurent하다면 message를 accept한다.
예제 ) p = 3119, e1 = 2, d = 127이고, e2 = 2^127 mod 3119 = 1702이다.
r = 307으로 선택하고, e1,e2,p를 public하게 announce하고 d 는 secret하게 두었다.
M = 320을 보낼 것이다.
S1 = e1^r mod p = 2^307 mod 3119 = 2083
S2 = (M-d*S1)*r^-1 mod 3118 = 2105
이제 Alice는 Bob에게 M,S1,S2를 전송한다.
V1 = e1^320 = 2^320 = 3006
V2 = d^S1 * S1^S2 = 1702^2083 * 2083^2105 = 3006
V1과 V2는 congruent하므로, accept한다.
4) Schnorr Digital Signature Scheme

이전의 ElGamal digital signature scheme의 문제점은 p가 매우 커야 한다는 것이다. p가 최소한 1024비트가 될 것을 권장한다. 이는 signature이 2048비트 이상으로 만들어지게 된다. signature 크기를 줄이기 위해서 ElGamal을 based한 새로운 scheme이 제안되었다.
Siging process
: two function이 two signatures를 만든다.
Verifying process
: one function의 output과 S1을 비교한다.
이 scheme에서는 two moduli ; p and q를 쓴다. f1과 f3은 p, f2는 q를 쓴다.

message를 signing하기 전에, Alice는 key를 generation해야 한다.
1. Alice는 prime p를 선택하고, usually 1024 bits in length로 선택한다.
2. Alice는 다른 prime q를 선택하는데 same size as the digest created by cryptographic hash function을 고른다. prime q는 p-1을 divide할 수 있어야 한다. 즉 (p-1) = 0 mod q이다.
3. Alice는 e1 = e0^((p-1)/q) mod p 로 선택한다.
4. integer d를 private key로 선택한다.
5. e2 = e1^d mod p 로 계산한다.
6. 이제 alice의 public key는 (e1,e2,p,q)가 되고, private key는 d가 된다.
Signing
1. Alice는 random number r을 선택한다. Alice는 new message를 보낼때 마다 r을 변경해야 할 필요가 있다. r은 1에서 q까지의 수중 고른다.
2. aLICE는 s1 = H(m|e1^r mod p)를 계산한다. 즉 메시지 뒤에 e1^r mod p가 append되는 것이다. 그리고 hash function을 통해 digest를 생성한다.
3. Alice는 second signature인 S2 = r+d*Si mod q를 계산한다.
4. Alice는 M,S1,S2를 전송한다.
Verifying
1. bob은 V = h(M|e1^S2 * e2^(-S1) mod p) 를 계산한다.
2. S1가 V modulo p와 congruent 하다면 message는 accept된다.
5) Digital Signature Standard(DSS)

DSS는 ElGamal scheme을 based로 한 digital signature algorithm(DSA)를 이용한다.
Signing process에서 두 function은 두개의 signature을 생성한다.
Verifying process에서는 output of one function과 S1을 비교한다. 마치 Schnorr과 비슷하다. 하지만 입력값이 다르다.
Key Generation
Signing을 시작하기 전에 Alice는 key generate를 할 필요가 있다.
1. Alice는 prime p를 선택하고, 이는 512~1024비트 길이이다. number of bits in p는 64의 배수여야 한다.
2. Alice는 160bit prime q를 선택하고, q는 (p-1)을 divide할 수 있어야 한다.
3. Alice는 two multiplicative group <Zp*,X>, <Zq*,X>를 쓴다. 후자는 전자의 sub-group이다.
4. Alice는 e1 = e0^((p-1)/q) mod p 를 계산한다.
5. Alice는 private key d를 선택하고 e2 = e1^d로 계산한다.
6. Alice의 public key는 (e1,e2,p,q)가 되고, private key는 d이다.

Signing
1. Alice는 random number r(1<=r <= q)를 선택한다.
2. Alice는 S1 = (e1^r mod p) mod q를 계산한다. 이 첫번째 value S1은 message M에 independent하다.
3. Alice는 message digest h(M)을 생성한다.
4. Alice는 second signature S2 = (h(M) + d*S1)*r^-1 mod q를 계산한다.
5. Alice는 M,S1,S2를 전송한다.
Verifying
1. Bob은 0<s1<q인지 check한다.
2. Bob은 0<s2<q인지 check한다.
3. Bob은 들어온 M으로부터 message digest h(M)을 계산한다.
4. Bob은 위 그림에서와 같이 V를 계산한다.
5. 만약 S1이 V와 Congruent할 경우 accept된다.
예제 ) q = 101, p= 8081, e0 = 3, e1 = 3^(8080/101) mod 8081 = 6968
d = 61을 선택하고 e2 = e1^d mod p = 2038으로 계산된다.
이제 public key는 (6968,2038,8081,101)이 되고, private key d = 61이다.
h(M) = 5000이라 가정하고 r = 61을 선택하자.
S1 = (e1^r mod p) mod q = 54
S2 = ((h(M) + d*S1)*r^-1) mod q = 40
이제 alice는 S1,S2,M을 Bob에게 전송한다.
S2^-1 = 48 mod 101
V = 54가 되고
S1과 V는 congruent하기에 accept한다.
DSS vs RSA
: DSS signature의 연산이 같은 p값에서 RSA보다 빠르다.
DSS vs ElGamal
: DSS signature이 ElGamal signature보다 작다. q가 p보다 작기 때문이다.
6. Variation and Applications
1) Time Stamped Signatures
: 가끔 signed document가 time stamp를 필요로 할때가 있는데 adversary에 의해 replay되는것을 방지할 때이다. 이는 time-stamped digital signature scheme이라 불린다.
2) Blind Signatures
: Sometimes we have a document that we want to get signed without revealing the contents of the document ot the signer.
'학교공부 > 암호공학' 카테고리의 다른 글
| [암호공학] 15장. Key Management (0) | 2019.12.05 |
|---|---|
| [암호공학] 14장. Entity Authentication (0) | 2019.12.01 |
| [암호공학] 12장. Cryptographic Hash Functions. (0) | 2019.11.29 |
| [암호공학] 11장, Message Integrity and Message Authentication (0) | 2019.11.28 |
| [암호공학] 10장. Assymetric-Key Cryptography (0) | 2019.11.26 |